REPRESENT

There's a reason I don't go that much into representational origami. Sure, I love it and I think it is completely amazing... But every time I try my hand at it I completely fail. I always think that the next time I should be able to do a little better than the last since I've had some practice from the time before, but that's never the case. Regardless, here I am, continuing the battle against making 'realistic' things out of paper.

These are old, but I thought I'd share them.

Maybe another reason I'm less about representational origami is because the geometry isn't as apparent (I mean, of course it's there but it doesn't slap you in the face like a nice tessellation or modular piece does). That said, the amount of incredible mathematical equations, terrifying algorithms and... other crazy math things I don't think I'll ever be able to wrap my brain around is fantastic! Maybe that's why I'm so bad at them.

I'll keep practicing and hopefully I'll be able to fold  a paper dragon battling a paper phoenix amongst paper smoke in a paper thunderstorm one day....

PAPER DONUT

At last, the long awaited post #101. Here she is, I'll skip right to the good stuff.

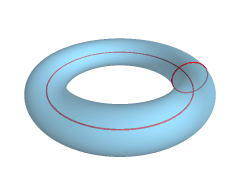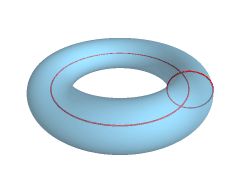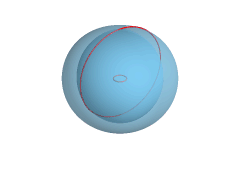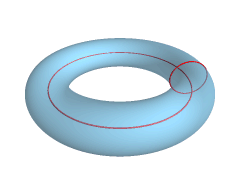
Came across this lovely paper design by Maria Garcia Monera and Juan Monterde (pattern here + the coolest flickr ever). 24 crescents come together to form a delightfully mesmerizing donut shape - or more accurately, a 'torus'. I found great joy in learning about this geometric surface which is created by a 2D closed circle (or curved shape) revolved around an axis to form a 3D solid. Cool stuff right there. Well, here's a paper torus and I like it a lot. *Apologies for the out of focus image, it's not easy to drop what you're doing to take process shots when you're as excited as I was*

Mathy!